Sinus,Cosinus ableiten ǀ Lernwerk TV

Ableitung Cosinus • einfach erklärt · [mit Video]

Die Ableitung von -sin(x) ist -cos(x) und die Ableitung von -cos(x) ist sin(x). Diese Ableitungen folgen direkt aus den Ableitungsregeln für Sinus und Cosinus sowie der Regel, dass die Ableitung einer Funktion, die mit einer Konstanten multipliziert wird, gleich der Konstante multipliziert mit der Ableitung der Funktion ist.

Mathelernen mit Martin BIFIEBeispiel 1_010 Ableitung von Sinus und CosinusFunktion YouTube

Schritt 1: Schreibe den Cosinus hin und in den Cosinus die Funktion ( innere Funktion ): f' (x) = cos (2x + 5). Schritt 2: Bestimme die Ableitung der Funktion im Sinus: (2x + 5)' = 2. Schritt 3: Schreibe die Ableitung aus Schritt 2 mit einem Malpunkt hinter den Cosinus: f' (x) = cos (2x + 5) • 2. Fertig!

Die Ableitung vom Sinus ist wirklich der Kosinus grafisch erklärt YouTube

Der Ableitungsrechner berechnet online Ableitungen beliebiger Funktionen - kostenlos! Mit diesem Online-Rechner kannst du deine Analysis-Hausaufgaben überprüfen. Er hilft dir beim Lernen, indem er dir den kompletten Rechenweg anzeigt. Der Ableitungsrechner kann die erste, zweite,., fünfte Ableitung berechnen.

Kettenregel anwenden [Beispiele] Einfach 1a erklärt

2.1K. 82K views 2 years ago Alles rund ums MATHE ABI. Ableitung Sinus Cosinus Kettenregel In diesem Mathe Lernvideo erkläre ich (Susanne) wie man die Trigonometrischen Funktionen Sinus und.

ABLEITUNG Sinus Cosinus Kettenregel viele Beispiele YouTube

Die Ableitung von Kosinus ist Minus Sinus. f (x)= \cos (x) f (x) = cos(x) f' (x)=-\sin (x) f ′(x) = −sin(x) Die Ableitung vom Tangens lautet: f (x)= \tan (x) f (x) = tan(x) f' (x)=\dfrac {1} { (\cos (x))^2} f ′(x) = (cos(x))21. Trigonometrische Funktionen ableiten Definition.

Ableiten von Trigonometrische Funktionen Sinus Kosinus YouTube

f(x) = -15 * sin(x) + 7 * cos(x) f'(x) = -15 * cos(x ) - 7 * sin(x) Erklärung: Die Koeffizienten -15 und 7 bleiben jeweils erhalten; sin(x) abgeleitet ergibt cos(x); cos(x) abgeleitet ergibt -sin(x); somit ergibt sich für den ersten Teil der Funktion -15 * cos(x) und für den zweiten Teil 7 * - sin(x); anders dargestellt auch -7 * sin(x)

Ableitung Sinus und Kosinus YouTube

Kosinus: Funktion, Ableitung und Stammfunktion. Tangens: Funktion, Ableitung und Stammfunktion. Kotangens: Funktion, Ableitung und Stammfunktion. Sekans: Funktion, Ableitung und Stammfunktion. Kosekans: Funktion, Ableitung und Stammfunktion. Sinusquadrat: Funktion, Ableitung und Stammfunktion. Kosinusquadrat: Funktion, Ableitung und Stammfunktion.

Ableitung der trigonometrischen Funktionen Sinus und Cosinus inkl. Übungen

Die Ableitung der Kosinusfunktion. Kennt man bereits die Ableitung der Sinusfunktion, kann man (\cos (x))' (cos(x))′ mit der Kettenregel ausrechnen. Verschiebt man den Graphen der Sinusfunktion um \frac {\pi} {2} 2π nach links, erhält man die Kosinusfunktion. Das bedeutet: \cos (x)=\sin\left (x+\frac {\pi} {2}\right) cos(x) = sin(x+ 2π).

Sinus, Cosinus, Umkehrfunktionen und Hyperbelfunktionen ableiten online lernen

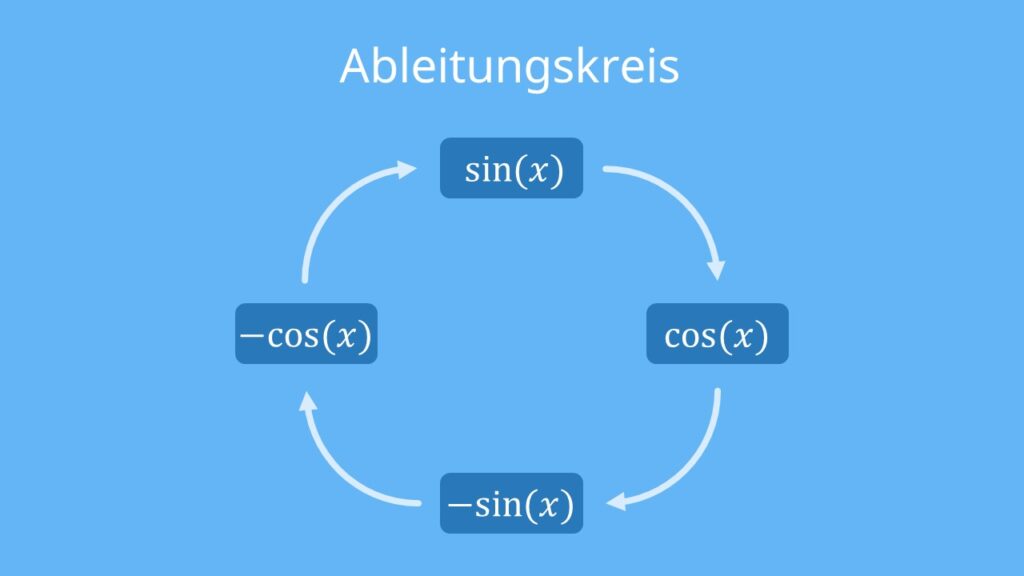
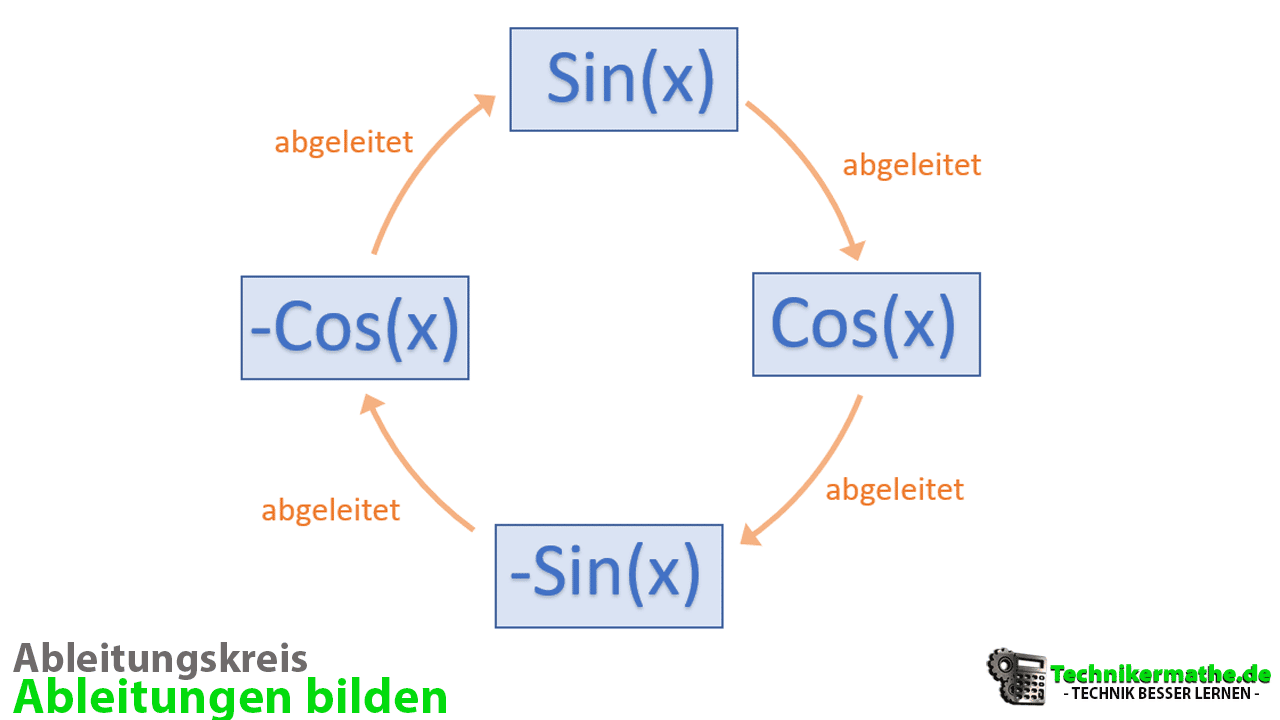
Die Ableitungen der Sinus- und Kosinusfunktion kannst du dir als eine Art Kreislauf vorstellen. Dazu kannst du dir folgende Abbildung anschauen: Abbildung 1: Ableitungskreis Sinus- und Kosinusfunktion. Wenn du dir diesen Kreislauf merkst, hast du schon einmal einen wichtigen Großteil der Ableitungen verstanden.

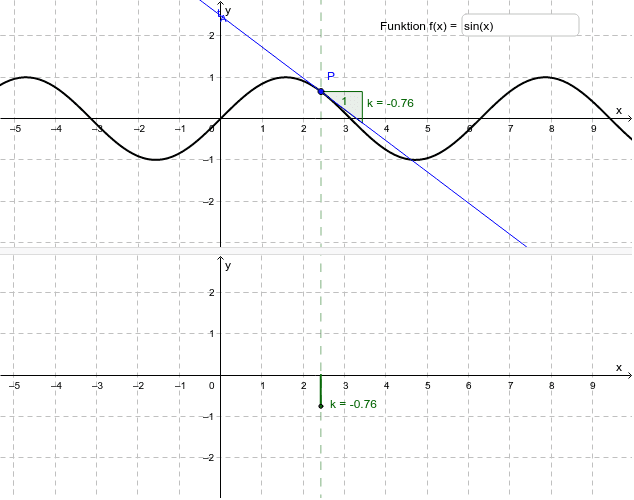
Grafisches Ableiten bei Sinus und Cosinus GeoGebra

Ableitung von Sin (x) und Cos (x) sowie Kettenregel und Produktregel einfach erklärt (Mathe Abi] - YouTube. MatheViBe. 402 subscribers. Subscribed. 361. 5.1K views 2 years ago. In diesem.

Sinus, Cosinus, Umkehrfunktionen und Hyperbelfunktionen ableiten online lernen

$f(x) = -9\cdot sin(x)$: Der Koeffizient $-9$ bleibt erhalten und die Ableitung von sin(x) ist cos(x). Daher lautet die Ableitung insgesamt; $f'(x)=-9 \cdot cos(x)$ $f(x)=5x-cos(x)$: Hier wird jeder Term einzeln abgeleitet. Die Ableitung von $5x$ ist $5$, die Ableitung von $cos(x)$ ist $-sin(x)$. Die Ableitung lautet insgesamt also $f'(x) = 5.

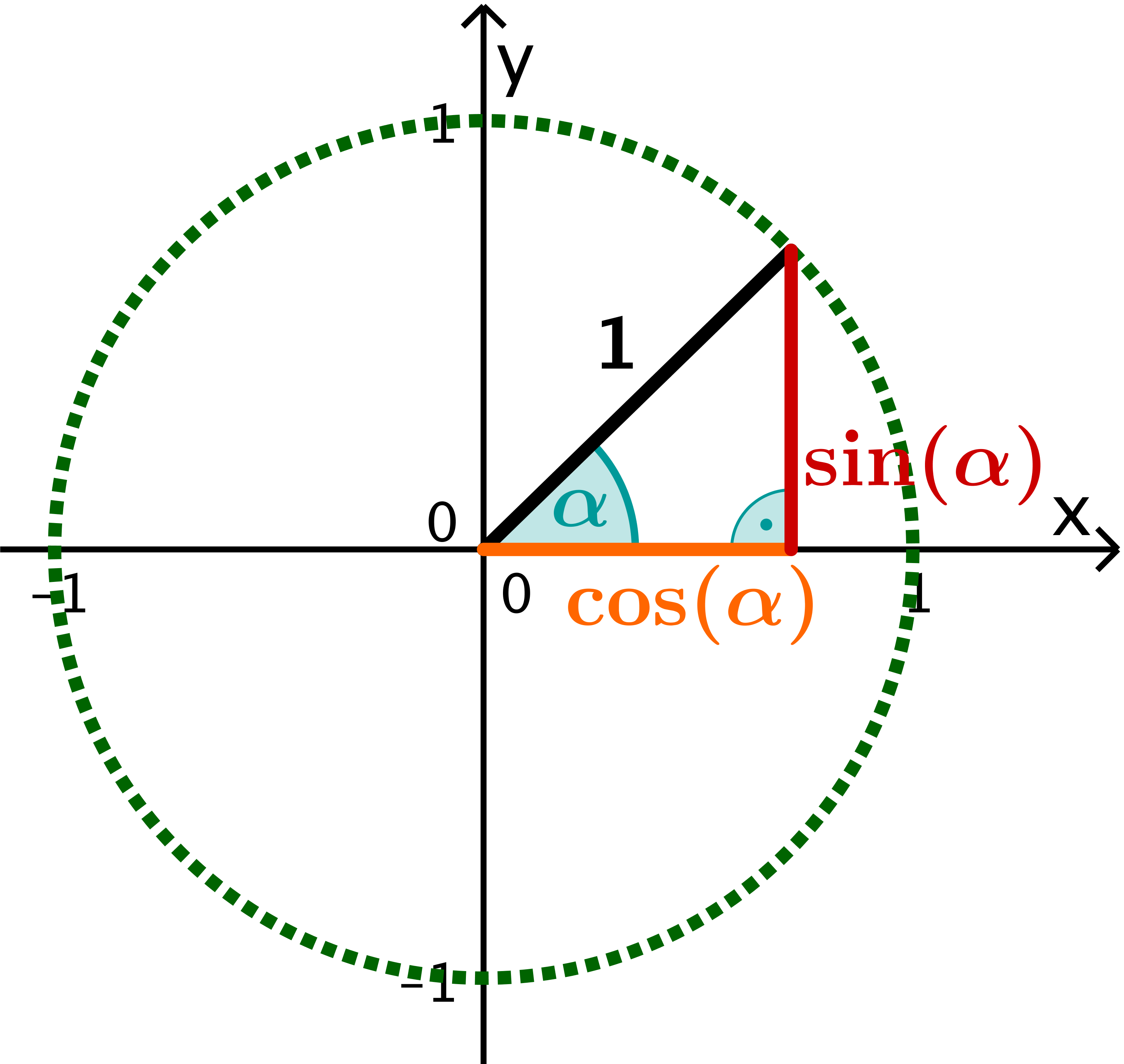
Trigonometrie am Einheitskreis lernen mit Serlo!

Trigonometrische Funktionen abzuleiten bedeutet, die Ableitungen von Sinus, Cosinus und Tangens zu berechnen. Erfahre, wie sie mit Ableitungsregeln kombiniert werden können und welche Besonderheiten es gibt. Inhaltsverzeichnis zum Thema Trigonometrische Funktionen ableiten. Trigonometrische Funktionen. Ableitung von Sinusfunktionen.

19 Die Ableitungen von Sinus und Cosinus YouTube

Beweis, dass cos ( x) die Ableitung von sin ( x) ist. Erklärung. Ableitung mit Hilfe des Differentialquotienten durchführen. f ( x) als sin ( x) umschreiben. Sinus mit Hilfe des trigonometrischen Additionstheorems umschreiben. Faktorisieren. Grenzwert in zwei Grenzwerte durch den Grenzwertsatz umschreiben.

Ableitung von Sinus und Kosinusfunktion (EF Kw4) YouTube

Trigonometrische Funktionen ableiten, sin(x) cos(x)Wenn noch spezielle Fragen sind: https://www.mathefragen.de Playlists zu allen Mathe-Themen findet ihr auf.

maxresdefault.jpg

Erklärungen. Analysis. Differentialrechnung. Ableitung Cosinus. In diesem Kapitel schauen wir uns an, was die Ableitung vom Cosinus ist. Inhaltsverzeichnis. Formel. Beispiele. Online-Rechner. Erforderliches Vorwissen. Was ist eine Funktion? Was ist eine Ableitungsfunktion? Ableitungsregeln. Formel.

Sinus,Cosinus ableiten ǀ Lernwerk TV

Die Ableitung vom Sinus ergibt die Cosinus Funktion. Ableitung von f (x)=sin (x) f (x)= sin(x) ergibt: f' (x)=cos (x) f ′(x) = cos(x) Beispiel 1. Berechne die Ableitung der Funktion. f (x)=sin (2x) f (x) = sin(2x) Lösung: Wir haben es hier mit einer verketteten Funktion zu tun. f (x)=g (h (x)) f (x) = g(h(x))